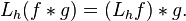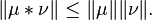In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the carrier signal, with a modulating signal that typically contains information to be transmitted.
In telecommunications, modulation is the process of conveying a message signal, for example a digital bit stream or an analog audio signal, inside another signal that can be physically transmitted. Modulation of a sine waveform transforms a baseband message signal into a passband signal.
A modulator is a device that performs modulation. A demodulator (sometimes detector or demod) is a device that performsdemodulation, the inverse of modulation. A modem (from modulator–demodulator) can perform both operations.
The aim of analog modulation is to transfer an analog baseband (or lowpass) signal, for example an audio signal or TV signal, over an analog bandpass channel at a different frequency, for example over a limited radio frequency band or a cable TV network channel.
The aim of digital modulation is to transfer a digital bit stream over an analog bandpass channel, for example over the public switched telephone network (where a bandpass filter limits the frequency range to 300–3400 Hz) or over a limited radio frequency band.
Analog and digital modulation facilitate frequency division multiplexing (FDM), where several low pass information signals are transferred simultaneously over the same shared physical medium, using separate passband channels (several different carrier frequencies).
The aim of digital baseband modulation methods, also known as line coding, is to transfer a digital bit stream over a baseband channel, typically a non-filtered copper wire such as a serial bus or a wired local area network.
The aim of pulse modulation methods is to transfer a narrowband analog signal, for example a phone call over a wideband baseband channel or, in some of the schemes, as a bit stream over another digital transmission system.
In music synthesizers, modulation may be used to synthesise waveforms with an extensive overtone spectrum using a small number of oscillators. In this case the carrier frequency is typically in the same order or much lower than the modulating waveform (see frequency modulation synthesis or ring modulation synthesis).
Analog modulation methods
In analog modulation, the modulation is applied continuously in response to the analog information signal.
List of common analog modulation techniques
Common analog modulation techniques are:
- Amplitude modulation (AM) (here the amplitude of the carrier signal is varied in accordance to the instantaneous amplitude of the modulating signal)
- Double-sideband modulation (DSB)
- Double-sideband modulation with carrier (DSB-WC) (used on the AM radio broadcasting band)
- Double-sideband suppressed-carrier transmission (DSB-SC)
- Double-sideband reduced carrier transmission (DSB-RC)
- Single-sideband modulation (SSB, or SSB-AM)
- Single-sideband modulation with carrier (SSB-WC)
- Single-sideband modulation suppressed carrier modulation (SSB-SC)
- Vestigial sideband modulation (VSB, or VSB-AM)
- Quadrature amplitude modulation (QAM)
- Double-sideband modulation (DSB)
- Angle modulation, which is approximately constant envelope
- Frequency modulation (FM) (here the frequency of the carrier signal is varied in accordance to the instantaneous amplitude of the modulating signal)
- Phase modulation (PM) (here the phase shift of the carrier signal is varied in accordance with the instantaneous amplitude of the modulating signal)
Digital modulation methods
In digital modulation, an analog carrier signal is modulated by a discrete signal. Digital modulation methods can be considered as digital-to-analog conversion, and the corresponding demodulation or detection as analog-to-digital conversion. The changes in the carrier signal are chosen from a finite number of M alternative symbols (themodulation alphabet).
According to one definition of digital signal, the modulated signal is a digital signal. According to another definition,the modulation is a form of digital-to-analog conversion. Most textbooks would consider digital modulation schemes as a form of digital transmission, synonymous to data transmission; very few would consider it as analog transmission.
Fundamental digital modulation methods
The most fundamental digital modulation techniques are based on keying:
- PSK (phase-shift keying): a finite number of phases are used.
- FSK (frequency-shift keying): a finite number of frequencies are used.
- ASK (amplitude-shift keying): a finite number of amplitudes are used.
- QAM (quadrature amplitude modulation): a finite number of at least two phases and at least two amplitudes are used.
In QAM, an inphase signal (or I, with one example being a cosine waveform) and a quadrature phase signal (or Q, with an example being a sine wave) are amplitude modulated with a finite number of amplitudes, and then summed. It can be seen as a two-channel system, each channel using ASK. The resulting signal is equivalent to a combination of PSK and ASK.
In all of the above methods, each of these phases, frequencies or amplitudes are assigned a unique pattern of binary bits. Usually, each phase, frequency or amplitude encodes an equal number of bits. This number of bits comprises the symbol that is represented by the particular phase, frequency or amplitude.
If the alphabet consists of 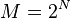 alternative symbols, each symbol represents a message consisting of N bits. If the symbol rate (also known as the baud rate) is
alternative symbols, each symbol represents a message consisting of N bits. If the symbol rate (also known as the baud rate) is 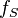 symbols/second (or baud), the data rate is
symbols/second (or baud), the data rate is 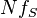 bit/second.
bit/second.
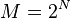 alternative symbols, each symbol represents a message consisting of N bits. If the symbol rate (also known as the baud rate) is
alternative symbols, each symbol represents a message consisting of N bits. If the symbol rate (also known as the baud rate) is 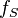 symbols/second (or baud), the data rate is
symbols/second (or baud), the data rate is 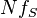 bit/second.
bit/second.
For example, with an alphabet consisting of 16 alternative symbols, each symbol represents 4 bits. Thus, the data rate is four times the baud rate.
In the case of PSK, ASK or QAM, where the carrier frequency of the modulated signal is constant, the modulation alphabet is often conveniently represented on a constellation diagram, showing the amplitude of the I signal at the x-axis, and the amplitude of the Q signal at the y-axis, for each symbol.
Pulse modulation methods
Pulse modulation schemes aim at transferring a narrowband analog signal over an analog baseband channel as a two-level signal by modulating a pulse wave. Some pulse modulation schemes also allow the narrowband analog signal to be transferred as a digital signal (i.e., as a quantized discrete-time signal) with a fixed bit rate, which can be transferred over an underlying digital transmission system, for example, some line code. These are not modulation schemes in the conventional sense since they are not channel coding schemes, but should be considered as source coding schemes, and in some cases analog-to-digital conversion techniques.
Analog-over-analog methods
- Pulse-amplitude modulation (PAM)
- Pulse-width modulation (PWM) and Pulse-depth modulation (PDM)
- Pulse-position modulation (PPM)
Analog-over-digital methods
- Pulse-code modulation (PCM)
- Differential PCM (DPCM)
- Adaptive DPCM (ADPCM)
- Delta modulation (DM or Δ-modulation)
- Delta-sigma modulation (∑Δ)
- Continuously variable slope delta modulation (CVSDM), also called Adaptive-delta modulation (ADM)
- Pulse-density modulation (PDM)
Miscellaneous modulation techniques
- The use of on-off keying to transmit Morse code at radio frequencies is known as continuous wave (CW) operation.
- Adaptive modulation
- Space modulation is a method whereby signals are modulated within airspace such as that used in instrument landing systems.


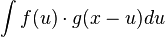

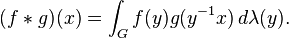
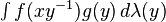 . The preference of one over the other is made so that convolution with a fixed function g commutes with left translation in the group:
. The preference of one over the other is made so that convolution with a fixed function g commutes with left translation in the group: